railway station puzzle

tackling the railway station puzzle - a quest for minimized cost

The Railway Station Puzzle

The Railway Station Puzzle aims to optimize the placement of railway stations to minimize the number of stations and the average travel cost for families. This problem is inspired by historical railway expansion, requiring efficient computational solutions. To understand the intricacies and rules of this puzzle, explore the problem statement on GitHub.

The problem as described in the README of the repository and in an attached PDF is a practical component of a course in my university, heard some collegues talking about it and decided to try.

Problem Definition

The task involves an NxM grid representing a map where each cell contains a number of families. The goal is to minimize the number of railway stations (A) and the average travel cost (B) to the nearest station. The travel cost is defined by distance with specified unit costs. The overall cost function is:

\[\text{Cost} = 1000A + 100B\]
Component Description
Objective Minimize the number of stations and the average travel cost
Initial State An empty grid with no stations
Possible Actions Place a station in any cell
Transition Model Update grid state with the new station placement
Cost Calculated based on the number of stations and the average travel distance
Successors All possible grids with one additional station
Solution Grid configuration that meets the objective with minimum cost
Constraints Average travel cost must be less than 3

Graph Representation

The problem is represented as a grid where each cell is a zone containing a number of families. The nodes are the zones, and edges represent the possible placements of stations.

This table succinctly encapsulates the problem’s components, providing a clear framework for the “Land Permutation Problem.” The constraints ensure that the number of borders in a successor state must not exceed that of the current state, guiding the search towards the objective.

Approach and Algorithms

Informed Search Algorithms

Informed search algorithms use heuristics to guide the search process, making them more efficient than uninformed search methods. These algorithms prioritize exploring paths that are more likely to lead to the goal, thus reducing the search space and time.

What is a Heuristic?

A heuristic is a technique used to estimate the cost of reaching the goal from a given state. It provides an educated guess based on available information, helping to prioritize certain paths over others.

Why Use Heuristics Instead of Cost?

Heuristics allow algorithms to make decisions based on estimated future costs, leading to more efficient searches. By using heuristics, informed search algorithms can quickly discard less promising paths, focusing computational resources on more likely solutions.

A* Algorithm

A* combines the actual cost to reach a node and the heuristic estimated cost to the goal, ensuring that the path found is both optimal and efficient.

How A* Works:

  1. Initialization: Starts from the initial node, using a priority queue to manage the frontier.
  2. Cost Function: Uses the evaluation function \(( f(n) = g(n) + h(n) )\), where \(( g(n) )\) is the actual cost and \(( h(n) )\) is the heuristic estimate.
  3. Node Expansion: Expands the node with the lowest \(( f(n) )\) value.
  4. Path Finding: Continues until the goal node is reached, ensuring the path with the minimum cost is found.

Best-First Search uses only the heuristic estimate to guide the search, always expanding the most promising node based on the heuristic value.

How Best-First Search Works:

  1. Initialization: Begins at the start node, with a priority queue to handle the frontier.
  2. Heuristic Evaluation: Uses a heuristic function \(( h(n) )\) to estimate the cost to the goal.
  3. Node Expansion: Prioritizes nodes with the lowest heuristic value.
  4. Efficiency: Can quickly find a solution, but may not always find the optimal path compared to A*.

Algorithm Selection

Informed search algorithms are chosen for their efficiency because they use heuristics to guide the search process. Unlike blind search methods, which explore all possible paths without direction, informed search algorithms focus on the most promising paths based on heuristic estimates. This reduces the search space and time required to find a solution. For the Railway Station Puzzle, using an informed search like Best-First Search ensures that both the number of stations and the average travel cost are minimized effectively, providing optimal results more efficiently.

Why Use Best-First Search for the Railway Station Puzzle

Best-First Search (BFS) is used in your Railway Station Puzzle implementation for several reasons:

1. Heuristic-Driven Efficiency

2. Memory Management

3. Implementation Suitability

Why Best-First Search Is Better for This Problem

1. Effective Heuristic Utilization

2. Reduced Computational Overhead

3. Flexibility in State Expansion

Conclusion

Best-First Search is a suitable choice for the Railway Station Puzzle because it leverages an effective heuristic to guide the search process, reducing the search space and computational overhead. By focusing on heuristic values, the algorithm can efficiently navigate towards solutions that minimize the total cost, making it a practical approach for this optimization problem.

Heuristic Selection

The heuristic used in this problem balances the number of stations and the travel cost:

\[\text{Heuristic} = \sum (\text{Families} \times \text{MinDistance}) \times \left(1 + \frac{\text{Number of Stations}}{\text{Total Families}}\right)\]

This ensures that the search process focuses on minimizing both the number of stations and the average travel cost, making it well-suited for the A* algorithm.

Implementation

To solve the Railway Station Puzzle, the problem was implemented in a structured manner using a Best-First Search algorithm. The solution includes:

Problem Modeling

The RailwayStation class represents the state space, defining the layout of the map, the placement of stations, and the cost calculations. The cost calculation is done using the formula provided in the problem statement, the heuristic is calculated using the formula provided above and a set is used to prevent states that are already in the queue of being added again (and having the cost of calculating the heuristic again). These are all fundamental for the algorithm.

Algorithms

In the implementation of the search algorithms we used the tools provided to us by java, we use a PriorityQueue to store the generated states after each interaction, and for this we also overriden the compareTo method in the state to use the heuristic. We also use a HashSet to keep track of the states already explored and since it has the states we overriden the equals and hashCode.

So on every iteration, we get the state with the best heuristic from the Priority Queue, we calculate its cost, check if it is a valid solution, if it is, we compare it with the best solution we have so far. Generate its children and add them to the priority queue. The algorithm goes on until all the state space is explored or until a minute or 100000 evaluations (of the cost), have been met.

Result Presentation

The DistanceMapViewer class visualizes the results using JavaFX. This class is responsible for presenting the map, station placements, and various statistics such as average cost, total cost, evaluations, and generations. The visualization provides a clear and interactive way to analyze the performance of the algorithm and the effectiveness of the station placements.

Color Coding of the Map:

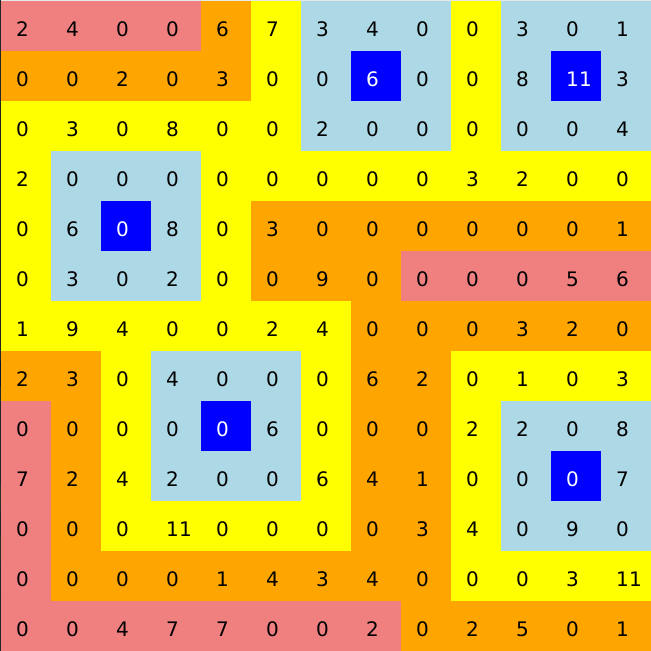
Results

The table below presents the outcomes of applying the Best-First Search algorithm to the Railway Station Puzzle across 20 different instances. Each entry includes the number of stations placed, the average travel cost, the total cost, the number of evaluations, the number of states generated, and the execution time.

Instance Stations Average Cost Total Cost Evaluations Generated States Execution Time
1 [[3, 1]] 2.48 1247 100000 101653 0s
2 [[2, 2]] 1.98 1197 100000 101009 0s
3 [[2, 3]] 2.95 1295 100000 114061 1s
4 [[3, 4], [6, 2]] 1.42 2141 100000 115284 1s
5 [[4, 3], [7, 6], [1, 2]] 2.28 3227 100000 184671 4s
6 [[6, 4], [1, 2]] 2.57 2256 100000 159621 2s
7 [[5, 4], [8, 7], [1, 6], [9, 2]] 2.71 4270 100000 280044 10s
8 [[3, 4], [3, 9], [4, 0]] 2.15 3215 100000 188545 4s
9 [[8, 4], [9, 11], [1, 7], [4, 2], [1, 11]] 2.93 5293 100000 425080 29s
10 [[5, 8], [7, 2], [1, 6], [9, 9]] 2.96 4296 100000 524928 17s
11 [[9, 5], [1, 9], [6, 1], [11, 10], [1, 2]] 2.70 5270 100000 459776 22s
12 [[8, 12], [3, 5], [10, 3], [6, 9], [12, 13]] 2.50 5249 100000 591103 26s
13 [[5, 10], [9, 15], [8, 3], [2, 8], [11, 7], [3, 1]] 2.31 6231 100000 651655 50s
14 [[4, 5], [6, 12], [11, 1], [12, 15], [5, 2], [3, 7]] 2.74 6273 100000 802805 32s
15 [[3, 15], [11, 5], [2, 7], [10, 15], [2, 2], [9, 8]] 2.97 6297 50278 722772 60s
16 [[7, 10], [10, 3], [9, 14], [2, 11], [4, 2], [9, 6]] 2.65 6265 100000 639612 35s
17 [[3, 14], [10, 4], [11, 15], [4, 3], [8, 11], [0, 8], [2, 17]] 2.57 7257 10510 810996 60s
18 [[8, 9], [2, 3], [4, 14], [9, 15], [8, 1], [10, 7], [4, 7]] 2.42 7241 100000 599432 43s
19 [[8, 12], [3, 4], [3, 13], [12, 9], [11, 15], [10, 2], [7, 17]] 2.68 7268 9909 592817 60s
20 [[8, 4], [7, 14], [13, 15], [1, 8], [1, 2], [9, 1], [4, 16]] 2.92 7291 6327 1252650 60s

Discussion

The results of the Best-First Search algorithm on the Railway Station Puzzle reveal several key points about its performance:

  1. Evaluation Consistency: Across all instances, the algorithm consistently performed 100,000 evaluations, indicating that it fully utilized the allowed computation budget in most cases.
  2. Execution Time: The execution times varied significantly, from 0 seconds to 60 seconds. The instances that reached the 60-second mark did not find an optimal solution within the time limit, suggesting increased complexity and larger state spaces in these cases.
  3. Generation of States: The number of generated states varied widely, from around 100,000 to over 1,250,000. This highlights the varying complexity of different instances and the corresponding impact on search space exploration.
  4. Solution Quality: The average travel costs ranged from 1.42 to 2.97, and the total costs ranged from 1197 to 7291. Instances with more stations generally had higher total costs but sometimes lower average costs, indicating a trade-off between the number of stations and travel efficiency.

The table provides a comprehensive overview of the algorithm’s performance, reflecting its strengths in efficiently exploring large search spaces and generating numerous potential solutions. However, the instances that hit the 60-second limit reveal areas where the algorithm struggles with time complexity, suggesting that further optimizations or alternative approaches may be needed for more complex scenarios.

Further Information

For readers interested in learning more about heuristic search algorithms and their applications, the following resources provide comprehensive explanations and examples:

These resources offer valuable insights and deeper understanding for anyone looking to expand their knowledge of heuristic search algorithms and their implementation in solving complex problems like the Railway Station Puzzle.